Velika triler diskusija maturanta i profesora oko priznavanja boda na maturi iz matematike

Nekolicina maturanata, među njima i oni koji su sudjelovali na državnim natjecanjima, javili su nam se oko zadatka 25.2 A razine državne mature. Smatraju kako je zadatak nejasno postavljen, a iznenadili su se katalogom rješenja u kojem je jasno da se traži dodatan uvjet za točan odgovor. Ipak, nekolicina profesora s kojima smo se pričali, govore kako maturanti nemaju jake argumente za žalbu, ali i da je zadatak mogao biti jasnije postavljen. Zadnju riječ će naravno imati NCVVO koji je dobio žalbe od maturanata.

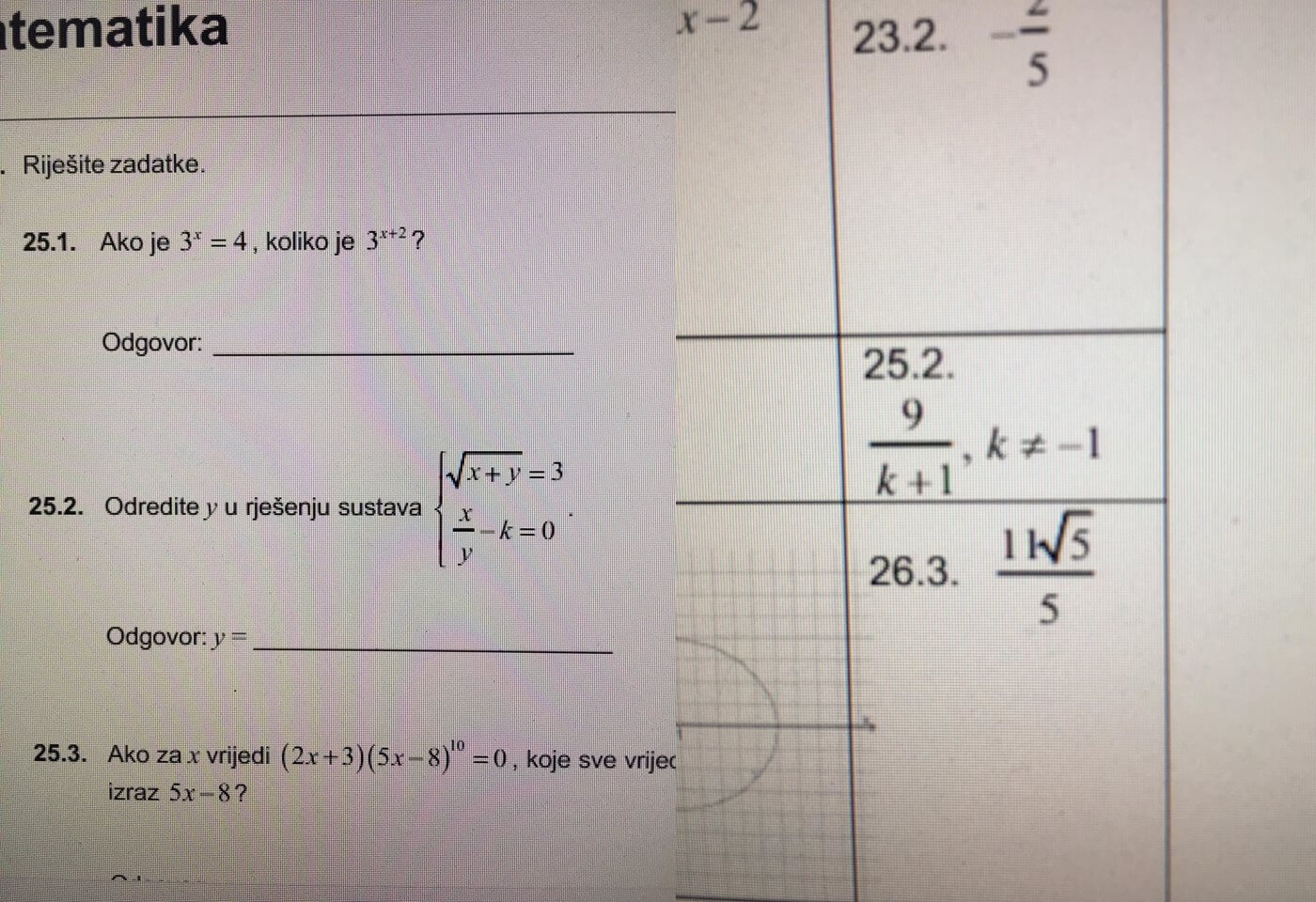
Matura 2018. – zadatak 25.2.2018.

“Slažem se da je zadatak mogao biti malo preciznije zadan, npr:

S druge strane, ovo kako je zapisan je prilično standardno (i u nastavi, i inače): najčešće se traži rješenje u najopćenitijem skupu brojeva za koji sustav ima smisla; to je u ovom slučaju skup realnih brojeva, R “, govori nam mladi profesor matematike sa Sveučilišta u Zagrebu koji nas je zamolio za anonimnost.

Tri argumenta maturanata i triler diskusija

Učenici koji su nam se javili tvrde kako sa zadatkom ima nekoliko problema, te ih argumentiraju.

– Prvi argument jest da u zadatku nije navedeno odakle su brojevi x,y,k. Teoretski tako mogu biti iz skupa N. Nije li onda greška izbaciti iz prirodnih brojeva broj koji tu ne pripada?, kažu nam maturanti.

Mladi profesor matematike tvrdi da je uistinu zadatak mogao biti malo precizniji, ali i da se i ovako više-manje podrazumijeva (pogotovo u srednjoj školi) da “riješite jednadžbu” ili “riješite sustav” znači riješiti u skupu realnih brojeva..

Npr, svi su u srednjoj školi jako puno puta vidjeli zadatak oblika: “Riješite jednadžbu x2 + x – 1 =0” i uvijek je nekako bilo implicitno da se traže realna (ili eventualno kompleksna rješenja).

‘Kako možemo uopće pričati o k=-1 kad za taj broj sustav nije definiran’

Maturanti nisu stali na ovome, imali su drugi argument za navodno krivo postavljeni zadatak.

– U zadatku je lijepo naglašeno da se nađe y kao rješenje sustava. Međutim za k=-1 sustav uopće nije definiran (jer bi bilo korijen iz 0 jednako 3). Kako onda možemo uopće pričati o k=-1 kad za taj broj sustav nije definiran. Tražimo rješenje sustava koji ne postoji, pitaju se naši maturanti.

Profesor matematike, kao u dobrom teniskom meču, ima odgovor i za ovo.

– Ovo je suptilno, ali ipak sve štima: nije da sustav nije definiran, nego nema rješenja, a to je ipak različito. Naime, zato  imamo sasvim jasno definiran sustav samo što on nema rješenja.

Maturanti u grčevitoj borbi za nagradu Soljačić gdje je svaki bod bitan

Maturanti ne posustaju i navaljuju s trećim argumentom u ovoj detaljnoj borbi koji bi pojedincima mogao otkinuti bod vrijedan borbe za nagradu Marin Soljačić.

– Autor zadatka sam ne navodi da je y različito od 0. Podrazumijeva li se to? Hmm. Zanimljivo. A zašto se nama ne podrazumijeva? Dvostruki kriteriji, tvrde maturanti.

U posljednjoj izmjeni argumentacije, servis ima profesor matematike.

– Slično kao u odgovoru na prethodno pitanje: zapravo se podrazumijeva. Naime “riješite sustav” znači “nađite sve parove brojeva (x,y) koji zadovoljavaju obje jednadžbe”. Posebno, zahtijevamo da ima smisla uvrstiti taj par (x,y) u jednadžbe. Dakle, ako za neku vrijednost (x,y) neka od jednadžbi nije definirana, smatramo da taj par (x,y) nije rješenje.

Konačno, mislim da bi najpotpuniji odgovor na pitanje u zadatku glasio ovako nekako:

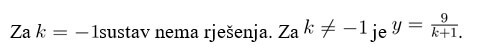
Ukupno mi se čini da nije ništa strašno krivo sa zadatkom/rješenjem, jedino da je moglo biti malo preciznije. Vjerojatno bi bilo bolje da je zadatak zadan preciznije, jer ovako se čini dosta strogo ako se oduzimaju (vrijedni:) bodovi za zaboravljenu napomenu, ali mislim da zapravo nije riječ o nečem dovoljno krivom za neku ozbiljniju žalbu, zaključuje ovaj triler profesor matematike .

Ali kako to biva, utakmica se igra do posebnog sučevog zvižduka, ili teniskom žargonom, dok oko sokolovo (NCVVO) ne kaže svoj pravorijek. Pojedini maturanti su nas pritom podsjetili na maturu 2012. godine iz koje su iskopali identičan zadatak. Te godine se priznavao bod za točan odgovor i bez dodatnog uvjeta.