[Mozgalica] Možete li riješiti vijetnamski zadatak za 8-godišnjake?
Učitelj matematike Tan Phuong iz Vijetnama odlučio je svojim 8-godišnjim učenicima postaviti naizgled lak aritmetički zadatak, a poslao ga je, kako kaže, i nekim osobama ‘s doktoratom iz područja ekonomije i matematike’. Možete li ga riješiti i vi?
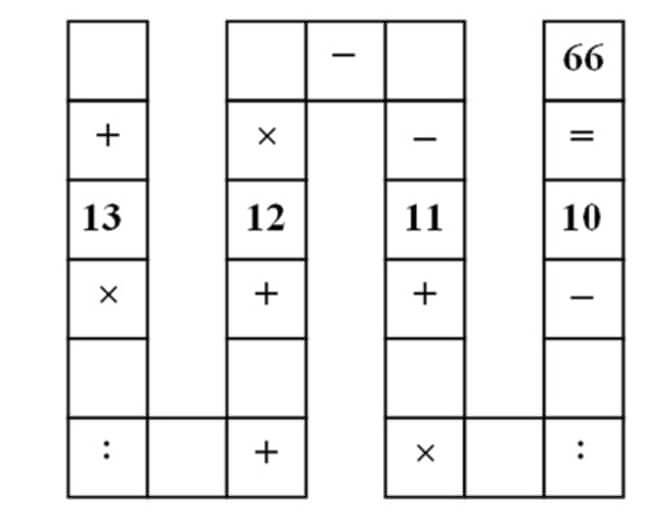
U prazna polja treba upisati brojeve od 1 do 9, koristeći svaki broj samo jedanput, kako bi jednadžba imala smisla, odnosno kako bi računskim operacijama dovela do broja 66.
PRIMJER RJEŠENJA (izvor t-portal)
Prije svega treba znati da se u ovom zadatku, kako bismo što prije stigli do cilja, trebamo koristiti određenim logičkim pretpostavkama te da mozgalicu možemo pretvoriti u sljedeću jednadžbu:
a + (13b/c) + d + 12e – f – 11 + (gh/i) – 10 = 66
Kao što je rečeno a, b, c, d, e, f, g, h i i će biti neki od brojeva iz niza 1, 2, 3, 4, 5, 6, 7, 8 i 9.
U prvom koraku -11 i -10 možemo prebaciti na drugu stranu jednadžbe. Oni će time promijeniti predznak i zbrojiti se sa 66 pa ćemo dobiti sljedeću uredniju jednadžbu:
a + (13b/c) + d + 12e – f + (gh/i) = 87
ili još ljepšu:
a + d – f + (13b/c) + 12e + (gh/i) = 87
Sada nam logika kaže dvije stvari:
1) da razlomci moraju biti cijeli brojevi i
2) da b/c ne smije biti preveliki broj kako se pomnožen sa 13 ne bi pretvorio u još veći.
Dakle, za pretpostaviti je da će b biti = 2, a c = 1 (kada bi bilo obratno ne bismo dobili cijeli broj). Tako dobivamo najmanji mogući okrugli broj za 13b/c i imamo sljedeći oblik jednadžbe:
a + d – f + 26 + 12e + (gh/i) = 87
Odnosno, ako 26 prebacimo na drugu stranu:
a + d – f + 12e + (gh/i) = 61
Budući da smo 1 i 2 potrošili, preostali su nam brojevi između 3 i 9. Među njima se nalaze tzv. primarni ili prosti brojevi 3, 5 i 7 koji su djeljivi samo sami sa sobom i sa 1 pa znaju zakomplicirati razlomke. Stoga je preporučljivo da ih se pokušamo riješiti u prvom dijelu jednadžbe koja ne sadrži razlomke.
Dakle, neka bude a = 3, d = 5, a f = 7.
Onda imamo:
3 + 5 – 7 + 12e + (gh/i) = 61
Odnosno:
12e + (gh/i) = 60
Preostali su nam još brojevi 4, 6, 8 i 9. Sada je potrebno malo se poigrati s njima, no to više nije tako puno brojeva. Ponovno vrijedi da e ne bi smio biti nijedan od većih brojeva jer bi već i 12 x 6 bilo više od 60, čak i bez (gh/i), pa je logično da je e = 4.
Dakle imamo:
48 + (gh/i) = 60
Sada je već jasno da mora biti da je gh/i = 12 iz čega slijedi jedino moguće:
g = 9
h = 8
i = 6
Ako ih uvrstimo u gornju jednadžbu, dobivamo:
48 + (72/6) = 48 +12 = 60
Ako pak redom uvrstimo sve od a do i u početnu jednadžbu, dobit ćemo 66. Naravno, ovaj zadatak ima više mogućih rješenja – neki od brojeva mogli su zamijeniti mjesta.
